高二的同學現在大概都正在和排列組合搏鬥當中吧!
下個禮拜就是期末考了
當然我的家教學生也不例外
而在接進大考的時候
他的情緒也就愈發的焦慮
對於變化多端的題型有著使不上力的情形發生
無法解決的題目形成了一直累積的壓力
其實一直以來這樣的情形另我感到訝異與不解
就我個人認為
在一直強調和現實經驗結合的現代中學數學教育風潮下
(時常聽到「你這樣沒辦法和學生經驗認知結合」)
排列和組合應該是對同學而言最貼近的數學知識
最常用來解決現實世界的問題
像是分組,排隊入坐,樂透還有點飲料,撲克牌
這些的問題都來自於現實生活可想像的到的部份
另我不解的是
同學對於這一方面的學習是相當被動的
被動的部分所指的是「思考」的部份
如何思考出一個完善的方法來描述這一個事件
那再從思考的方法換成數學式子
之後把解給找出來
在排列組合的訓練中我覺得最重要的是如果去思考建立一個流程
舉例來說
題目:3男4女選出2男3女排成一排,男生不相鄰的情形有幾種?
思考:3男中先找出2男,4女先找出3女,這選出的5個人隨便排再扣掉男生相鄰的情形。
算式: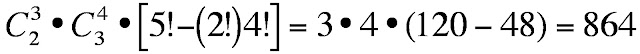
(其中的4!前的2!是指相鄰的男生可以左右交換有2!種)
像是這樣的一個思考流程是我覺得在學習排列組合中最重要的一個部份
如果想的完善完整是自我的一個挑戰
而很多同學覺得很難就放棄了思考
這是我覺得很可惜的一件事
因為除了數學考試之外
我們的人生不會是時常在評估某事的狀態?
當然世事是絕對不是課本上題目那麼單純的
那麼課本上的題目就顯的更重要了
從簡單的情形下著手去思考如何是完善的情況
我覺得這是排列組合這個單元的額外收獲
況且
在排列組合的學習過程中
我們常常可以發現同一個題目
不同的人會有不同的解法
計算過程會有些許的不同
了解之下才知道他人的思考路徑和我是不同的
同樣的在這個社會中
和我價值觀冏異的人多的是
我們若是能抱著開放的態度
接受他人也有自己一套的思考路徑
而非只堅持自己的看法
這也是在課程中時常出現的情形
更常出現的是「哇!怎麼能想到這樣,太誇張了。」
舉個例子:
題目:十顆號碼球從1~10,取出三顆完全不連號的情形有幾種?
思考:用排容原理,全部的情形-確定兩顆連號+三顆連號
算式: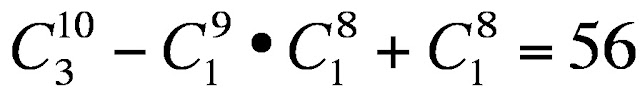
但是就是會有人想到這樣的方法,
思考:拿出十顆空白的球,現放下7顆,
剩下的三顆從這7顆所形成的8個空隙中插入
那這後放入的三顆球必不相鄰
再將號碼填入,那三顆球上的號碼即為不連號的一組號碼
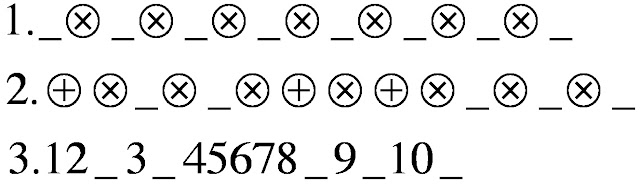
如上所選的號碼為(1,5,7)
算式: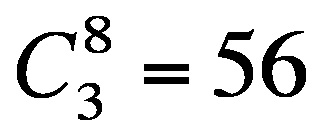
每個人看事情的角度高度都不同
是否願意學著用其他人的角度來看
或許會有意外的收獲
排列組合就是這樣的一個好東西(茶)
2008年1月13日 星期日
[家教]排列組合
訂閱:
張貼留言 (Atom)





3 回應:
hi你好
近日在學習排列組合,也看了你這篇的二個例子,所以有問題想請教你!
3男4女這題,看了你的解答不知後方的4!代
表的是什麼?
10顆球的,你提起全部情形-2顆連號+3顆連號, 為什麼要加3顆連號??
不好意思我算初學者,麻煩你指導一下^^
感恩
hi mei yin:
第一個問題~
5!-(2!)4!中的4!是什麼
整個解釋起來是
5!-->全部的排法
2!-->指相鄰的男生可以左右交換
4!-->是指兩個相鄰的男生視為一個元素,和另外三個女生共四個元素下去做排列,所以為4!。
第二個問題:
為什麼要把三個連號的加回來
我們可以找一個例子來說明
十個號碼球全部的情形-二個連號球
很明顯的因為有連號所以要減掉
所以我們可以先選連號的號碼12、23、...910,共九種然後再找一個數字和這個連號的元素配對,當然剩下的號碼就有8種,以上這些ok嗎?ok了就繼續以下的問題的核心了~
上面的選擇會出現一種情形
連號的選了 34 配對的號碼選5--->345
連號的選了 45 配對的號碼選3--->345
因為我們先選連號的號碼再選配對的號碼
所以儘管數字的結果是345是相同的
但是我們在減去的時候是將它視為不同的情況
所以就345這組號碼上我們就把它減去了兩次
那是不是就是應該把它加回來?
那是否每一組連號都會有這樣的情形?
123--> 12&3 1&23
234--> 23&4 2&34...以此類推
三個連號的號碼全都多減了一次
故要把三個連號的情形加回來
如果這個了解了那你的排容一定ok的^^
不知是否看的懂我的解釋呢?
HIHI
在你的講解後有清楚了,謝謝你!!
期許自己在你網站上能學些東西^^
張貼留言